
Trigonometry is not a huge part of the ACT math section. However, if you’re familiar with SOH-CAH-TOA and how to work through trigonometry questions, you’ll have no problem with the 4-6 trigonometry questions that show up on the exam, earning you some easy points. Here is a quick overview of the trigonometry information that we think you’d be smart to review during your ACT test prep, so you’ll be ready to work through pesky trig questions on test day.
Trigonometry is a branch of mathematics that studies relationships involving lengths and angles of triangles.
With trigonometry, you can use information about identified angles and sides of a triangle to find other unknown angles and sides.
If you’ve taken a high school geometry course, you’re probably familiar with SOH-CAH-TOA. SOH-CAH-TOA is how you take information you know about a triangle and use it to find information that you don’t know. Here is what SOH-CAH-TOA stands for:
All the equations above mean is that you start at a specific angle θ and consider the sides around it to determine the equation for the angle. The hypotenuse is obviously always going to be the triangle’s longest side. The side farthest from angle θ will be the “opposite” side, and the angle touching it is the “adjacent” side.
Consider a random triangle. If you know one side measure and one non-90° angle of a triangle, you can figure out the other sides and angles using trigonometry. If you know the lengths of two sides of a right triangle, you will be able to find the measure of all the interior angles using trigonometry.
When you’re given a geometry problem where you’re given two side lengths of a triangle and you have to find the third side, you can use Pythagorean theorem to find the missing side. But what if you only know one of the side lengths and one of the angles of the triangle? Even though we only have the length of one side, we can still find the others using trigonometry because we have the measure of one of the interior angles.
If I know the length of the hypotenuse and the length of the opposite side, I can use that information to find the angle measure of θ. Lets pretend the hypotenuse is 15 and the opposite side is 5. I can use the first equation above that utilizes both opposite and hypotenuse sides, and I would set this equation up like this:
Sin(θ) = 5/15
For the ACT, some questions will simply have you stop there — they want to see that you can set up the correct trigonometry equation to find a particular side. For other questions, they may require you to plug this equation into your calculator and get a specific value for the angle measure. Pay attention to the format of your answer options to make sure you’re not working too hard and solving the full equation if you don’t have to.
Lets take a look at how trigonometry sometimes looks when it makes an appearance on the ACT…
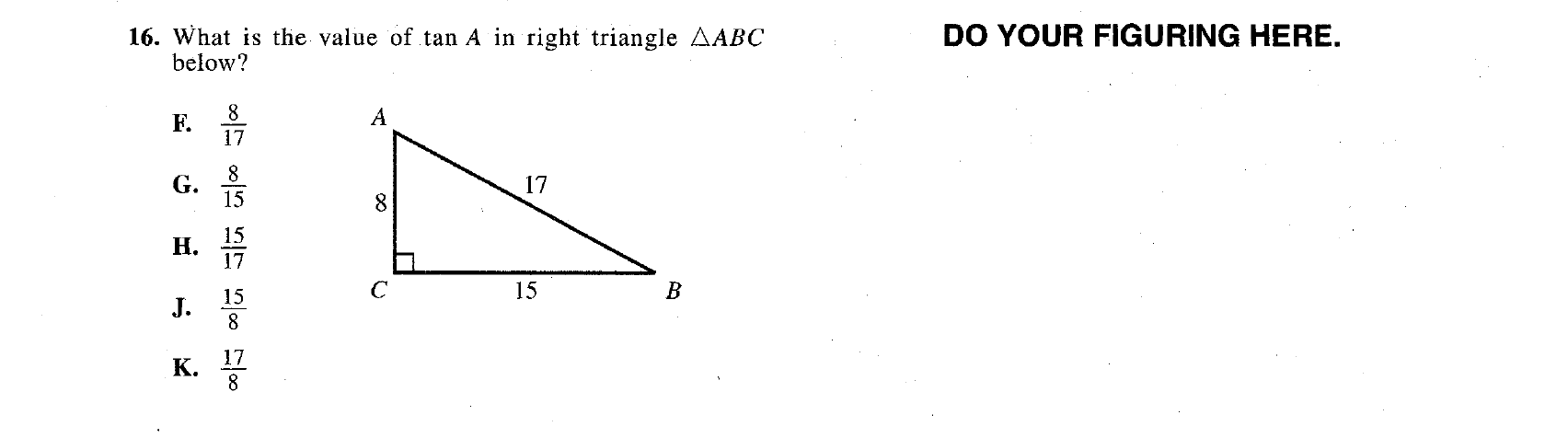
Question 16, above, is a nice, straightforward question as long as you know your SOH-CAH-TOA equations and how to use them.
The question is telling you to find tan(A). Therefore, you should start at angle A and consider your tangent equation:
tan(θ) = opposite/adjacent
From angle A, the opposite side is going to be 15 (the side farthest away), and the adjacent side is going to be 8 (the touching side that is not the hypotenuse). Therefore, your equation becomes: tan(A) = 15/8 — your correct answer for this question is J.
*Notice how easy it could be to accidentally select an incorrect side and get a different answer option for 16. It is VERY important to double-check your work on trigonometry problems because it is so easy to make small, avoidable errors.
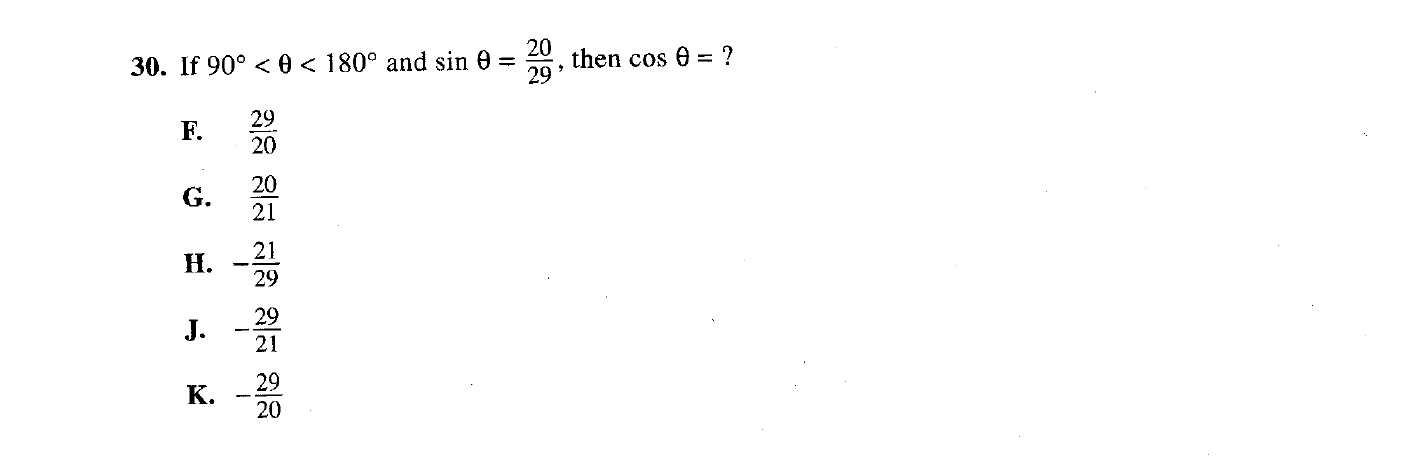
In question 30 above, you’re given the equation for sin(θ) and are tasked with finding cos(θ). If you’ve written out your 3 SOH-CAH-TOA equations, you know that SOH and CAH have something in common: they both have the hypotenuse value as their denominator.
Sin(θ) = opposite/hypotenuse
Cos(θ) = adjacent/hypotenuse
Since you’re given the equation for sin(θ)=20/29, you know that the hypotenuse has to equal 29. Therefore, you know that the denominator value in the cos(θ) equation will ALSO be 29. Take a look at your answer options. There is only one answer option that has 29 as the denominator value. Answer option H is the correct answer.
*Notice how this question did not require you to do any math or figuring with your calculator at all. Many of the earlier trigonometry questions that show up on the ACT will seem very simple and straightforward as long as you are familiar with the SOH-CAH-TOA equations. That is all they are testing you on with this equation: do you know SOH-CAH-TOA and how it works.
In question 29, above, you’re now given a story, a diagram, and some information about the triangle. Consider what you know about the triangle: 2 side lengths. Take a look at your answer options — you see sin, cos, and tan. This question is clearly asking you to use trigonometry.
However, this question looks a little different. They are using Arcsin, Arccos, and Arctan. Where does the Arc come from? Rather than looking for the value of a side (as with the earlier problems), this time you’re looking for the angle measure.
Your equation will start out looking like this: Sin(θ) = 2.5 / 8
Now think of the question like regular geometry. You need to get θ by itself to find out what its value is. You’re solving for θ. That’s where Arc comes into play. Arc is the inverse of the function. If you check out your calculator, you’ll probably notice that there are buttons that show sin^-1, cos^-1, and tan^-1. This is how you would plug in the equation to get an actual angle value. Here, however, you aren’t required to work that far, and you can stop once you’ve figured out the equation. The correct answer is B.
*Hint: You don’t really care about the story of this question. This is going to be true of many story problems that the ACT throws at you. Make sure you aren’t wasting precious time by reading and rereading story problem information that doesn’t actually matter. Rather than reading about Janelle over and over, pull out the information that you need from the story — numbers and values — the first time you read it to make sure you’re using your time wisely. For this question specifically, you don’t actually need any of the story information. The ACT has already input the values that you know for the triangle. You can simply focus on the diagram and the SOH-CAH-TOA part of the question.
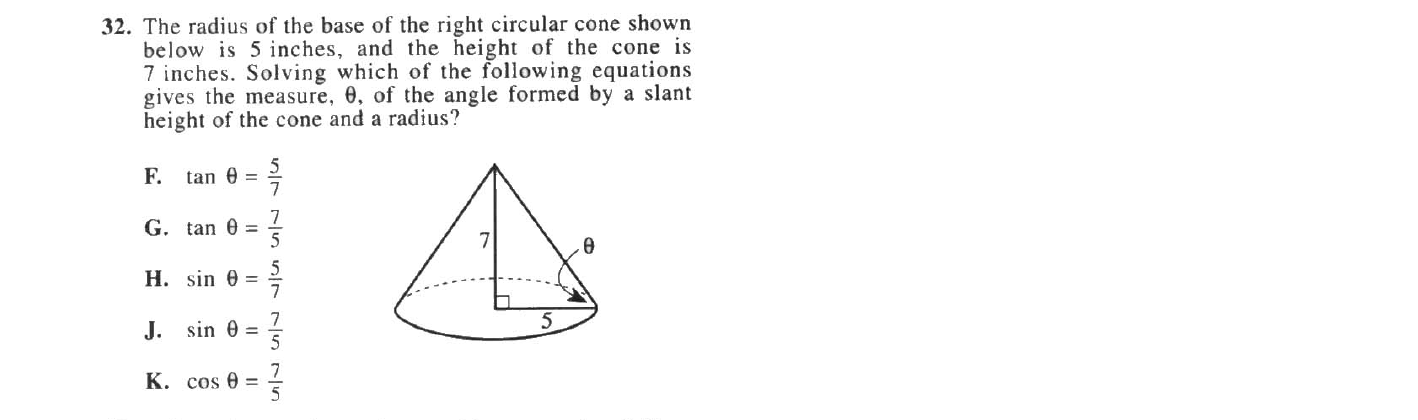
Question 32, above, once again gives you a diagram and an explanation. Once again, you are searching for the measure of angle θ, but this time you do not have to anything except set up the equation. No need to worry about inverse functions here — just write out SOH-CAH-TOA and figure out the equation.
This time you’re given the opposite (7) and adjacent (5) side values for θ. To find angle θ, you’d need to use tan(θ) = opposite/adjacent.
This equation would look like this: tan (θ) = 7/5
The correct answer is G.
*Once again, notice how this problem looked like it might be difficult, but it ended up being very simple. Don’t be intimidated by any of the problems in the ACT math portion — especially the trigonometry questions. Write out SOH-CAH-TOA and work through the question carefully, ensuring that you select the correct values for each slot.

Question 42, above, is a little bit different than the trigonometry questions that have come before it. There is no triangle, no diagram, and no side values. This is an example of a word-based trigonometry question, rather than one with actual data values.
This question is showing up as question #42, which means that it’s meant to be somewhat difficult. What they are really testing you on here is whether you realize that the sin(θ) value and cos(θ) value add up to 90°.
Take a look at this sample triangle:
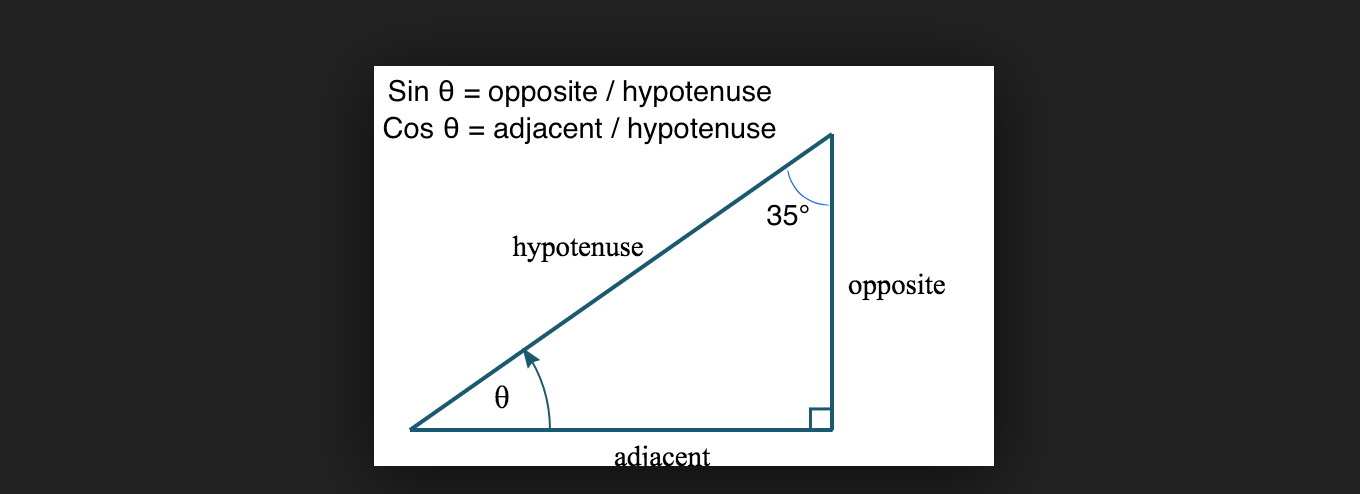
If we know that one angle of this triangle is 90°, then the other two angles MUST add up to 90° as well because the interior angles of all triangles will add up to 180°. We’ve plugged in 35° as one angle to show how then θ would have to be equal to 55°. 35+55 = 90.
Now look back up to question #42 -
The question is asking you to determine which answer option is NOT equal to sin x°. Consider each answer option:
F. -sin(-x°) — this is the same as sin(x°), so this answer is wrong
G. sin(-x°) — this is your correct answer
H. cos(90-x)° — we just looked at this principle above. Since sin x° and cos x° have to add up to equal 90°, this is the same as sin x°
J. cos(x-90)° — this is the same as J above
K. Square root of (1-cos x°) ^2 — this is the same as the square root of (sin x°) ^2 — this simplifies to just sin x°
*There will be few trigonometry questions that do not actually have you work with a triangle. In fact, you may not see a question like this at all, but if you do, know that you can work through it somewhat easily. Just remember the properties you know to be true of the triangles.
Write out SOH-CAH-TOA
It’s SO easy to make small, silly errors throughout the ACT math section. These are the worst type of errors because they can cost you so many precious points. Remember that every single question on the ACT is worth the same number of points on your score, so eliminating any silly errors you can will help your score tremendously. Rather than trying to work through trigonometry questions in your head and visualizing the three equations, write them out on your paper. By simply writing out SOH-CAH-TOA, you’re making sure that you have the equations straight, and you’re giving your brain a reminder that it can return to throughout the question. This eliminates so much room for error. There is nothing worse than doing all of the work right but using cos(θ) when you were meant to use sin(θ).
Use Process of Elimination
Process of elimination is a huge asset throughout all of the ACT sections, but it is especially important for the ACT math section. The math section is the only one where you have 5 answer options to select from instead of just 4. That means your probability of guessing correctly goes down significantly with the math section. Any wrong answers you can rule out will help you with making educated guesses on questions that you find difficult, as well as helping you work through questions you know how to do and narrowing down to the correct answer. For trigonometry, process of elimination can be pretty easy for most questions. Once you’ve figured out which function you need to work with — sin(θ), cos(θ), or tan(θ) — you will often be able to eliminate 2 or 3 wrong answers. Usually the ACT will not require you to actually solve the equation by plugging it into your calculator; the answer options will usually contain the equation all written out with the correct function. That means once you figure out that you need to use tan(θ), you can eliminate any answer options that use functions other than tan(θ).
Don’t work harder than you have to
Pay attention to the format of your answer options. Oftentimes trigonometry questions will require you to only set up the equation. Other times, you may be required to actually calculate the value of a side or angle and get a real number value as your answer. Make sure you work through the question toward the type of answer that the ACT is looking for. You don’t want to waste time finding the wrong type of answer or going farther than you have to.